You can make many mistakes while designing, running, and analyzing A/B tests, but one of them is outstandingly tricky. Called the “peeking problem,” this mistake is a side effect of checking the results and taking action before the A/B test is over.
An interesting thing about the peeking problem is that even masters of A/B testing (those who have learned to check if the observed difference is statistically significant or not) still make this mistake.
→ Test your product management and data skills with this free Growth Skills Assessment Test.
→ Learn data-driven product management in Simulator by GoPractice.
→ Learn growth and realize the maximum potential of your product in Product Growth Simulator.
→ Learn to apply generative AI to create products and automate processes in Generative AI for Product Managers – Mini Simulator.
→ Learn AI/ML through practice by completing four projects around the most common AI problems in AI/ML Simulator for Product Managers.
Statistical significance in simple words
Say you’re running an A/B test on 10 new users in your game, and you divide them randomly between the old and the new versions of the game. From the five users who got the old version of the game, two (40%) retained on the next day against three (60%) for the new version of the game.
Based on the collected data, can we say that the Day 1 retention rate of the new version of the game is better than that of the old version?
Not really. Our sample size is too small, so there is a high probability that the observed difference is accidental.
Statistics provides tools that help us understand whether the difference in metrics between the groups can be attributed to product changes rather than pure chance. In other words, it helps us determine whether the change is statistically significant or not.
A way to check the statistical significance based on the frequentist approach to probability taught at universities works as follows:
- We collect data for versions A and B.
- We assume that there is no difference between the two versions. This is called the null hypothesis.
- Assuming the groups are identical, we calculate the “p-value.” The p-value represents the probability of obtaining similar results if we repeat the experiment.
- If p-value is smaller than a certain threshold (usually 5%), we reject the null hypothesis. In this case, we can conclude with a high degree of certainty that the observed difference between the groups is statistically significant and is not due to chance.
- If p-value is greater than the threshold, we confirm the null hypothesis. This means the collected data does not show a significant difference between the tested versions of the game. In reality, however, there can be a difference between the versions. It’s just that the data we have doesn’t show it. A bigger sample size might yield different results.
This is a very simplified explanation of the basic idea behind determining whether the observed difference is statistically significant. In reality, things are more complicated: we need to study the data structure, clean the data, choose the right criterion, and interpret the results. This process contains many pitfalls.
A simple example of calculating statistical significance
Let’s get back to the game we discussed in the previous example.
The team decided to learn from the mistakes made in the first A/B test. This time they brought 2,000 new users to the game (1,000 to each version). On day 1, the first version retained 330 users against 420 for the second.
While the second version retained more users on day 1, the team wasn’t sure whether this was due to product changes or an accidental metric fluctuation.
To make it clear, the team had to calculate whether the observed difference in Day 1 retention was statistically significant or not.
In this case, we are looking at a simple ratio metric (the conversion of new users into taking a specific action – Day 1 retention rate), so we can use an online calculator to calculate statistical significance.
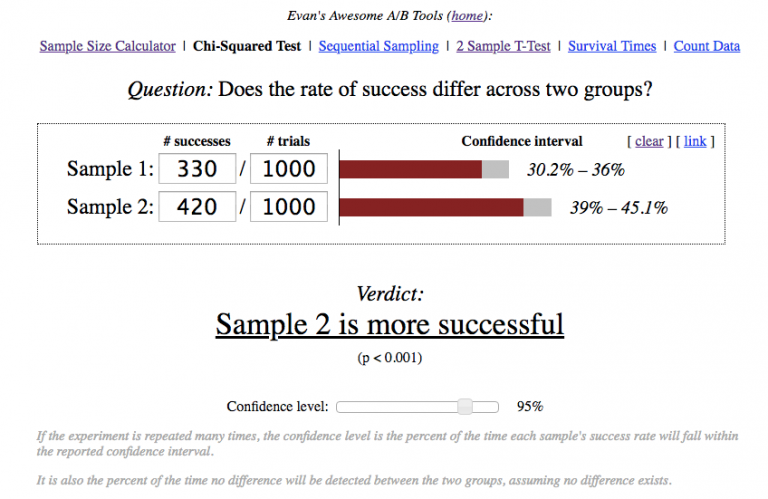
The calculator showed p-value < 0.001. That is, the probability of seeing the observed difference within the identical test groups is very small. This means that we can be sure that the increase in Day 1 retention rate is connected to the product changes we made.
Automated verification of A/B testing results with unexpected consequences
Encouraged by the progress made in the retention rate metric, the team decided to turn towards improving the monetization of the game. At first they decided to focus on increasing the conversion rate to first purchase. In two weeks, the new version of the game was put to an A/B test.
The developers wrote a script that checked the conversion rate of the first purchase in the test and control versions every few hours, and calculated whether the difference was statistically significant.
A few days later, the system spotted a statistically significant improvement in the conversion rate of the new version. The team thus thought of this test as successful and introduced the new version of the game to all the users.
You might have missed it, but there was a little mistake with big consequences that sneaked in while analyzing the test’s results. Let’s see what it was.
The peeking problem
To use different statistics criteria to calculate p-value in the approach requires meeting certain conditions. Many of them for example imply a normal distribution of the studied metric.
But there is another important condition that many people forget about: the sample size for the experiment must be determined in advance.
You must decide beforehand how many observations you need for your test. Then you should collect data, calculate results and make a decision. If you didn’t spot a statistically significant difference based on the amount of data you’ve collected, you can’t continue the experiment to collect additional data. The only thing you can do is run the test again.
The described logic might sound bizarre when viewed in the context of the real A/B testing companies run for internet services and apps, where adding new users to the test costs close to nothing and results can be observed in real time.
But the logic used for A/B testing within the framework of the frequentist approach to statistics was developed long before the Internet was made. Back then most of the applied tasks involved a fixed and predetermined sample size in order to test a hypothesis.
The Internet has changed the paradigm of A/B testing. Instead of choosing a fixed sample size before running the experiment, most people prefer to keep collecting data until the difference between the test and the control groups becomes statistically significant.
The original approach to calculating p-value does not work in this new experimental paradigm. In the case of testing things in this new way, real p-value becomes much bigger than the p-value that you get using the usual statistical criteria when checking the test results only once at the end of the experiment.
NB: The Peeking Problem occurs when you check the intermediate results for statistical significance between the control and test groups and make decisions based on your observations. If you fix the sample size at the beginning of the test and defer any decision to when you have the right amount of data, then there’s no harm in observing intermediate results.
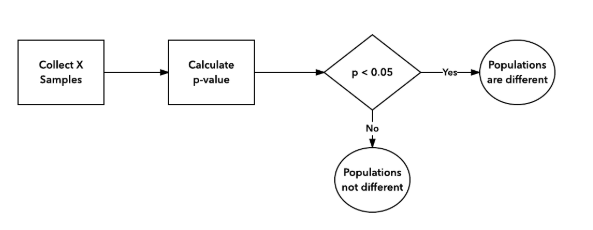
The correct A/B testing procedure (as part of the frequentist approach) is depicted in the following diagram:
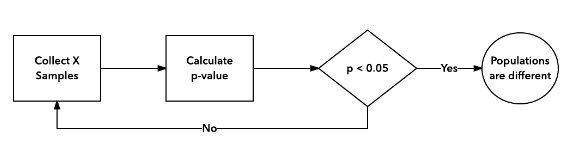
Incorrect A/B testing procedure:
Why Peeking increases p-value
Let’s go back to experiment with the first purchase conversion. Let’s suppose we know that in reality the changes we made to the game produced no effect.
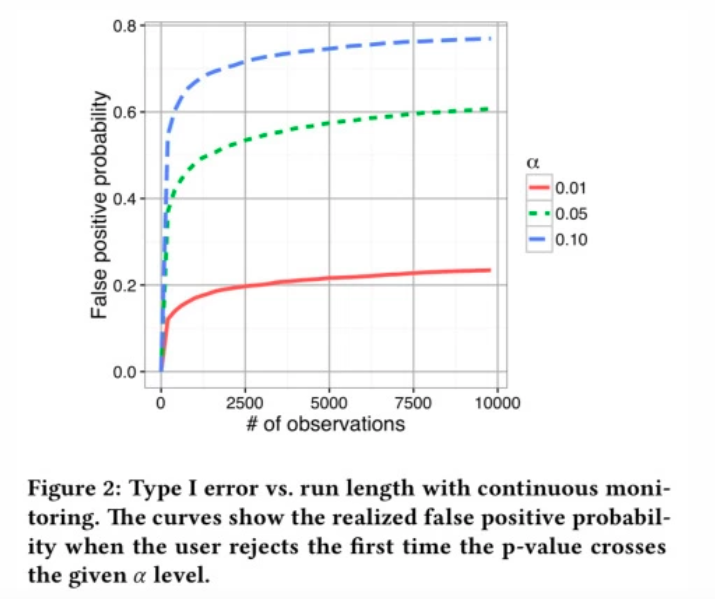
In the following graph you can see the dynamics of the difference in purchase conversion rates between the test and control versions of the product (blue line). The green and red lines represent the boundaries of the indistinguishability range, provided that the appropriate number of observations has been selected in advance.
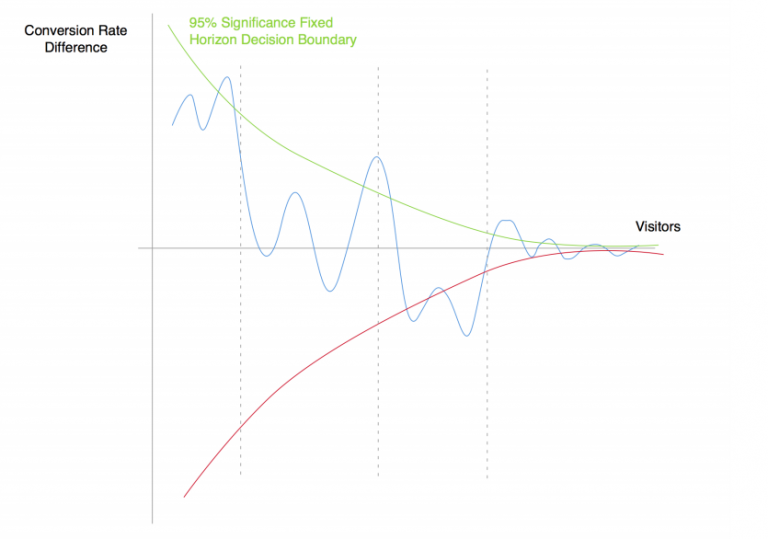
In the correct A/B testing process, we need to determine in advance the number of users needed for the test, collect observations, calculate the results and draw a conclusion. This procedure ensures that if the test is repeated many times, in 95% of cases, we will reach the same conclusion.
Everything changes greatly if you start checking the results frequently and are ready to act if you spot a difference. In this case, instead of asking whether the difference is significant at a certain predetermined point in the future, you ask whether the difference goes beyond the decision boundary at least once within the data collection process. Mind that these are two completely different questions to ask.
Even if the two groups are identical, the difference in conversion rates may sometimes go beyond the boundaries of the indistinguishability zone as we keep accumulating observations. This is totally OK, since the boundaries are built so that when testing the same versions, we can spot the difference in only 5% of cases.
Therefore, when you regularly check the results during a test and are willing to make a decision whenever there is a significant difference, you begin to accumulate the possible random moments when the difference falls out of the given range. As a consequence your p-value grows with every new “peek”.
If what we were talking about earlier is unclear, here is an example of how exactly peeking increases by p-value.
The effect of peeking at the p-value
The more often you look at the intermediate results of the A/B testing with the readiness to make a decision, the higher the probability is that the criterion will show a statistically significant difference when there is none:
- 2 peeking cases double the p-value;
- 5 peeking sessions increase the p-value by a factor of 3.2;
- 10,000 peeking sessions increase the p-value twelve-fold;
Options to solve the peeking problem
Fix sample size in advance and do not check results until all data is collected
This sounds very correct—but at the same time impractical. If you receive no signal from the test, then you have to start all over again.
Mathematical solutions to the problem: Sequential experiment design, Bayesian approach to A/B testing, lowering the sensitivity of the criterion
The peeking problem can be solved mathematically. For example, Optimizely and Google Experiments use a mix of Bayesian approach to A/B testing and Sequential experiment design to solve it (note that previously, we discussed everything within the framework of the frequentist approach; read more about the difference between Bayesian and frequentist approaches following the links at the end of this article).
For services like Optimizely, this is a necessity, as their value comes down to the ability to determine the best option based on the regular A/B testing check-ups on the fly. Feel free to read more here: Optimizely, Google.
There are many discussions in the tech community about the pros and cons of the described methods. In case you want to explore them in depth, the links at the end of this article provide more details.
A product-minded approach with a soft commitment to test time and correction for the essence of the peeking problem
When working on a product, your goal is to get the signal you need to make a decision. The logic described below is not ideal from a mathematical perspective, but it solves our product task.
The essence of the approach comes down to a preliminary assessment of the required sample to identify the effect in the A/B test as well as taking into account the nature of the peeking problem while making intermediate check-ups. This minimizes the negative consequences one may face when analyzing the test results.
Before starting the experiment, you need to evaluate what size of sample you need in order to see a change—if there exists one—with a reasonable probability.
Aside from the peeking problem, this is a useful exercise, because some product features require such large samples to identify their effect that there is no point in testing them at the current product development stage.
With the previously calculated sample in mind, once the experiment is launched, you need to (I’d say you must) monitor the dynamics of changes, but avoid making decisions when the difference first enters the statistical significance zone (as we already know of the peeking problem).
You need to continue to monitor what is happening. If the difference remains statistically significant, then, most likely, there is an effect. If it becomes indistinguishable again, then it isn’t possible to draw a conclusion about whether there is an improvement.
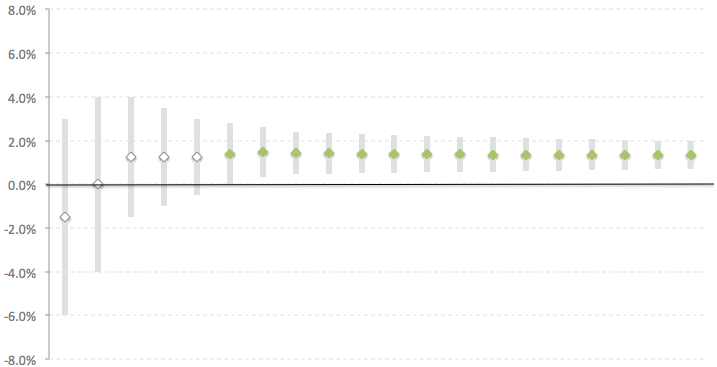
Let’s take a look at the results of two experiments demonstrated below, each of which lasted 20 days. Each point on the graph represents the relative difference in the metric between the test and the control version at the end of the corresponding day with a confidence interval. If the confidence interval does not cross zero (i.e. identical to the condition p-value <x), then the difference can be considered significant (if you select the appropriate sample in advance). The green diamonds are points in the experiment where the data showed a statistically significant difference between the two versions.
In the first experiment, starting from day 6, the difference between the versions became significant and the confidence interval no longer crosses 0. Such a stable picture gives a clear signal that the test version works better than the control one with a high degree of probability. Interpreting the results is not difficult.
In the second experiment, we can see that the difference sometimes crosses into the statistical significance zone, but then again dips back into irrelevance. If we did not know about the peeking problem, then we would have finished the experiment on day 4, assuming that the test version showed better results. But the proposed method for visualizing the dynamics of the A/B test in the course of time shows that there is no stable measurable difference between the groups.
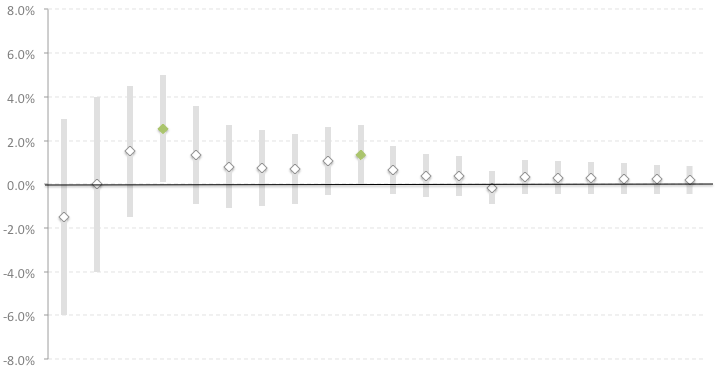
There are some controversial cases where it is difficult to interpret the results clearly. There is no single solution to the following cases, and it usually depends on the amount of risk you are willing to take and the cost of such a decision:
- Ordinary experiments where you test different features or small changes, and are ready to make a decision with a greater degree of risk.
- Expensive decisions when, for example, you try to test a new product development vector. In this case, it makes sense to analyze and study the data in detail. Sometimes you can run an experiment again.
Some will say that the described logic is an oversimplification and cannot be trusted. This could be true from a mathematical standpoint. But from a product/growth point of view it sounds quite reasonable.
When teams start to do more math than product work, it may be a signal that the effect of the changes made is too small or absent. But math won’t solve this problem, I am afraid.
Summing up
If the peeking problem sounds a bit convoluted and confusing, here’s one key takeaway that can guide you:
If you conduct an A/B test and at some point the test group difference becomes statistically significant, don’t end the experiment right away, believing that you have a winner. Keep watching. It also makes sense to pre-select the sample size, collect your observations, and then calculate the results based on them.
Extra resources
- Here is a good essay about the peeking problem.
- Another essay worth reading regarding the peeking problem. Mind that it contains the wrong idea that using the Bayesian approach may solve the Peeking problem.
- Comparison between Bayesian and frequentist approaches put in simple words.
- Another article arguing the Bayesian A/B testing is not immune to the peeking problem. It also discusses how different A/B testing services on the market are solving the problem.
- A discussion of the pros and cons of Bayesian vs frequentist approaches towards math statistics on Reddit.
- An article from Optimizely about their approach to solving the peeking problem.
- A lot of interesting things about Sequential analysis for A/B testing – at this link, at that one and here, too.
- This essay tells about how p-value grows when monitoring results with a willingness to make a decision.









