Product managers or analysts will often say something like: “My analysis of the data shows that users who do action X are more likely to buy the premium version or become successful.” Based on this insight, they decide to invest time and effort into making more users do X.
But this is a classic example of assuming causation where there is only correlation. Maybe one thing really does cause the other—or maybe it’s just another case of two metrics happening to grow at the same time.
We have all heard the time-old caution: “Correlation does not imply causation.” It sounds obvious, almost too obvious. Yet time and again, even very experienced people, whether by accident or design, treat them as the same thing.
Here we will look at why it’s so easy to gloss over the difference between correlation and causation, how to prove causality, and why it’s important to keep all this in mind when working on a product.
Many of the insights and examples below have been contributed by experienced product managers we spoke with for this article.
- Aishwarya Ashok (Product Manager – Early Team at Zoho; Co-Founder at TheProdcast; Product Mentor at adplist.org)
- Bhargav Sathish (Senior Associate, Product Manager at Capital One, Co-Founder & Innovation Director at The Earth Hacks Foundation)
- Rishal Sharma (Senior Product Manager, London Stock Exchange Group (LSEG))
→ Test your product management and data skills with this free Growth Skills Assessment Test.
→ Learn data-driven product management in Simulator by GoPractice.
→ Learn growth and realize the maximum potential of your product in Product Growth Simulator.
→ Learn to apply generative AI to create products and automate processes in Generative AI for Product Managers – Mini Simulator.
→ Learn AI/ML through practice by completing four projects around the most common AI problems in AI/ML Simulator for Product Managers.
Correlation and causation
When we say correlation, we refer to a relationship between two variables in which a change in one is accompanied by a change in the other. The key word here is “accompanied”, because a change can happen without either variable directly affecting the other.
If there is a proven direct effect of one variable on the other, then we have causation.
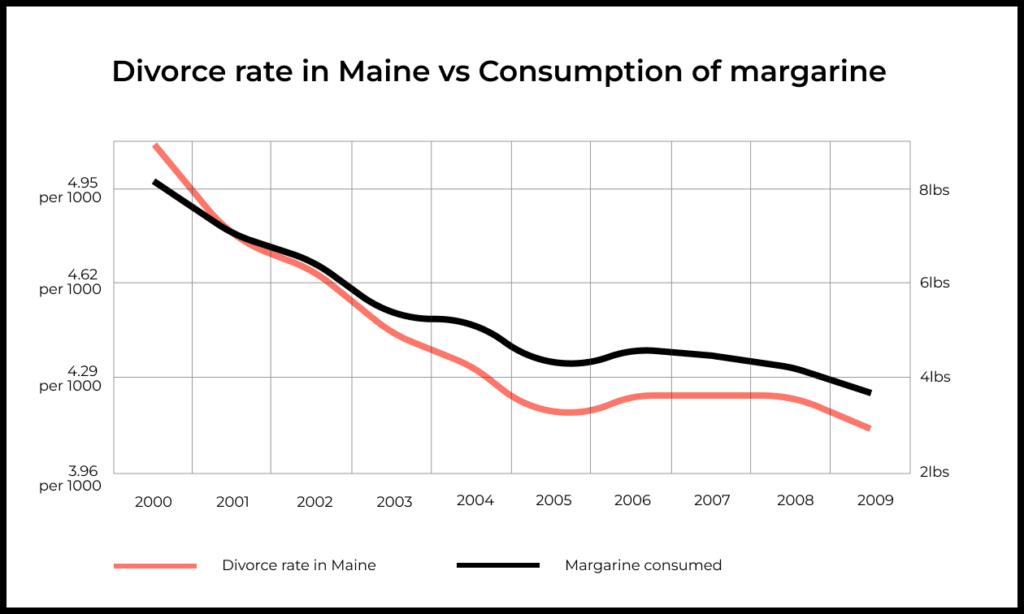
Take the example of correlation below. If we falsely assume causation, reducing consumption of margarine should reduce divorces in Maine, which would be… odd.
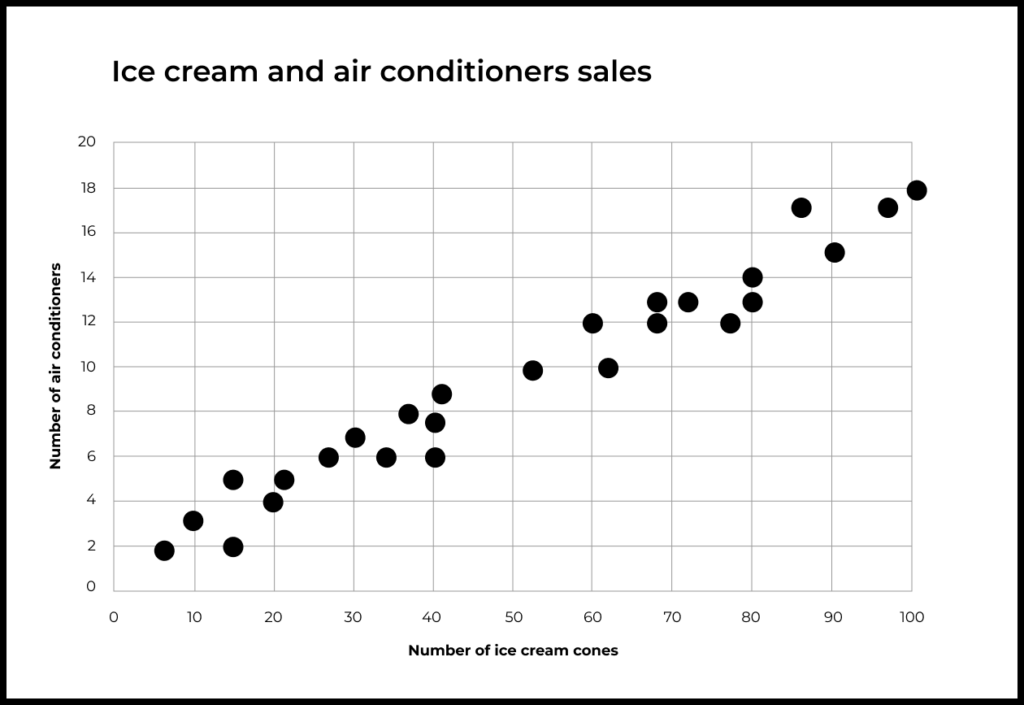
The first simple example that comes to mind is one that I read on Khan Academy, where a person collected data on the sales of ice cream and air conditioners sold in his city.
He found that when the sales of ice cream were low, the sales of air conditioners were also low. When the sales of ice cream were high, the sales of air conditioners were also high. From this data, we can conclude that there is a correlation between the sales of ice cream and air conditioners. To take it a step further, we can define this as a positive correlation (when the sales of ice cream go up, the sales of air conditioners are also going up).
However, just because there is a positive correlation between the sales of ice cream and air conditioners does not mean that selling more ice cream would cause more sales of air conditioners. In this scenario, there could be other factors that can cause the increase in sales for ice cream and air conditioners, such as an increase in temperature.
Bhargav Sathish, Senior Associate, Product Manager at Capital One, Co-Founder & Innovation Director at The Earth Hacks Foundation
What differentiates correlation from causation
Correlation can happen for different reasons. Perhaps the two variables are actually influenced by a third factor, like with ice cream and air conditioners. In the above example, that third factor is the summer heat.
With correlation, it’s not always possible to identify other factors capable of affecting both variables. Sometimes there might not be any. In that case, we should consider random chance. This is the case with divorces in Maine and margarine consumption, which is an example of spurious correlation.
What makes correlation different from causation?
Causation is a subset of correlation, i.e., all causations are correlations. However, the inverse is untrue (not all correlations are causations). Causation could be defined as a relationship between two variables where the existence of one would cause an effect on the other.
Since correlation is a statistical measure, it is possible that during experimentation or analysis you might find that drinking coffee and increase in Instagram followers are correlated. However, it would be unwise to think one causes the other without digging deeper into its analysis. Statisticians and Data Scientists often find themselves in this predicament.
Rishal Sharma, Senior Product Manager, London Stock Exchange Group (LSEG)
A correlation might result from random chance. But causation, by definition, cannot be random.
If there is correlation, then we need two more conditions to prove causality:
- No outside third factor affecting both variables
- Sequential timing of changes in the first and second variable (event A is followed by event B)
We’ll say it again: the difference between correlation and causation can seem obvious. But it’s so easy to mix them up in practice.
Examples of correlation confused with causation
Let’s look at a few examples of how correlation leads people to wrongly assume causation in real-life situations.
In the book “Thinking, Fast and Slow”, Daniel Kahneman describes his experience at a lecture for Israeli pilots. One instructor insisted that the pilots do a better job after getting harshly criticized for their mistakes. Kahneman proposed an experiment: pilots should try to hit a chalk target on the floor by tossing a coin twice without looking. Pilots whose first throw was good (close to the target) tended to do worse on their second throw, but their second throw was better if their first throw was bad.
Kahneman’s experiment was a vivid demonstration of regression to the mean. Whenever a pilot makes a very good or very bad throw, this is highly likely to deviate from their mean result. So their next throw will probably be closer to the mean (in the sense of better or worse than the first throw).
So it wasn’t in-your-face criticism that helped pilots to improve after a failure, but regression to the main. When results coincidentally improved after his feedback, the instructor mistook this correlation for causation.
Some widespread social beliefs also come down to correlation masquerading as causation. Take, for example, the idea that childhood music lessons improve cognitive abilities, memory, and attention span later in life. There may be a correlation between these factors, but we cannot claim causation given the huge number of confounding factors.
One of these factors is that music lessons cost money. So if a family has the resources to meet a child’s basic physical needs as well as afford special lessons, the child likely has access to better nutrition, schooling, and other favorable conditions for developing their intellect.
Here’s another example of correlation-that’s-not-necessarily-causation. An article in The Washington Post concluded that growing expenses on policing in the U.S. have failed to reduce crime. Because of the seeming absence of a direct correlation, the author claims to disprove causality between two events: an increase in police budgets does not lead to a proportional reduction in crime rates.
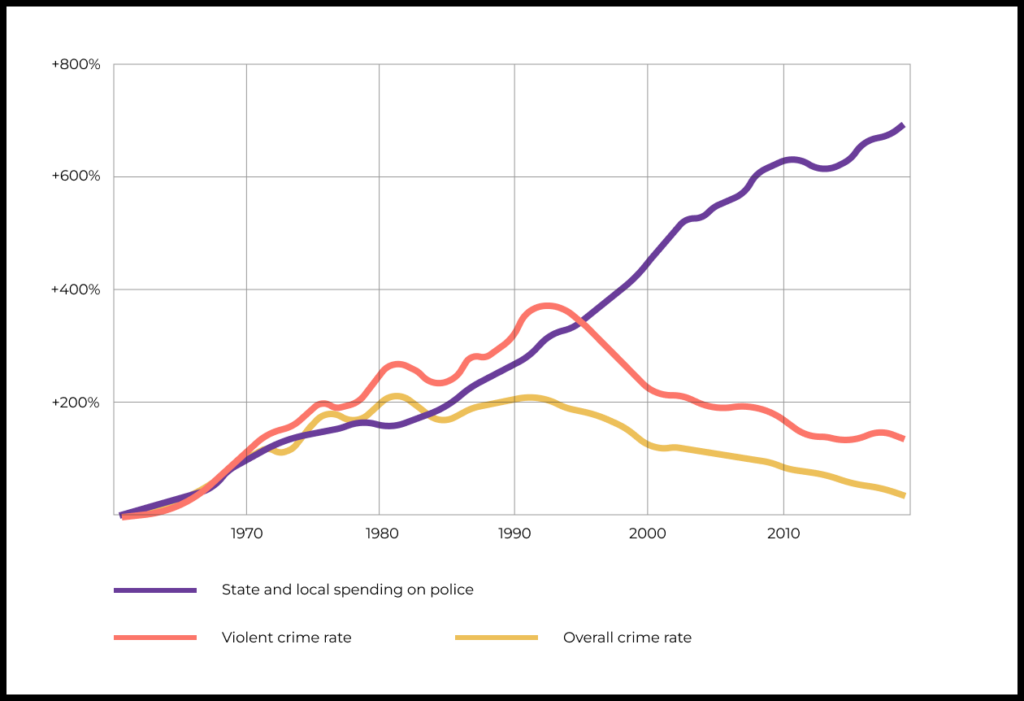
This mere fact does not give us enough information to prove or disprove the author’s claim, however. Perhaps rising crime is driving policing expenses, for example. Without more careful study we cannot say either way.
Correlation in business
In 2013, eBay spent tens of millions of dollars on ads for web searches containing the word “eBay”. The company was sure that this purchased traffic was driving sales up. But research showed that the advertising was targeting the same audience that would have made purchases on eBay anyway.
There was actually a third factor, user intent to make a purchase, causing both display of the search ad and the user’s purchase on eBay. Yet at eBay, they mistakenly thought they had found a cause (ad) and effect (purchase).
Confusing correlation with causation is a common mistake when analyzing the success of other companies’ products. “Product A took off and gained product/market fit thanks to feature X. We can recreate that success for ourselves if we add the same feature to our product in our own local market.”
Let’s assume that product A really did become successful after that other company added feature X. But we still don’t know that adding that feature is what made the product successful. Success is usually too complicated to be reduced to a single cause. But the main thing is that for a given user segment, the product has to perform a certain job better than all of the available competitors.
For example, WeChat Pay became massively popular for payments in China, but not because it combined chat with a mobile wallet. The reason is that it offered such a compelling alternative to cash that its added value was enormous, which made the product so successful.
If we keep this in mind, we can understand why Facebook Messenger had such a hard time adding payments. Simply bolting on functionality to a pre-existing chat platform wasn’t enough for the U.S. market, where electronic payments were relatively mature. This made the added value of Facebook-enabled payments minimal or non-existent to users.
Correlation in products
Product teams have to constantly think about the causes of changes in various metrics. It’s usually very tempting to explain these changes with something that we did recently and consciously. But we cannot forget that the product and users do not exist in a vacuum.
Example with sudden influx of users
When you have an increase in sign-ups (X) and you also released a new messaging feature (A), chances are that they’re correlated.
But X is caused by the fact that your competitor’s prices increased (B) last week and your pricing plans suddenly seemed affordable. And your sales team doubled down on this and closed more deals (C) and hence more sign-ups.
So X is correlated with A, but also correlated with C which is caused by B.
Aishwarya Ashok, Product Manager – Early Team at Zoho; Co-Founder at TheProdcast; Product Mentor at adplist.org
Example with mobile game monetization
Working on a mobile game, we might notice that users who link their social networks to the game make more purchases. So it could be very tempting to assume causality: that by increasing the rate at which players connect with social networks, we can proportionally increase earnings from such users. If this is true, then we could make a number of hypotheses for how to target this metric.
But in reality, in a situation like this, there can easily be one or multiple factors that are affecting both variables. We might fail to see that if a user is active with social networks and makes more purchases, maybe they are just more motivated and interested in the game to begin with. Maybe social networks don’t impact their behavior, but simply reflect the user’s pre-existing attitude toward the game.
If that’s true, then there is no point in nagging users to connect with social networks. At the same time, we can’t assume that it’s false. To find out, we have to perform an experiment.
How experiments prove causation
Superstitions, pseudo-science, and outdated treatment methods owe much of their prevalence to confusion between correlation and causation. Examples include rainmaking and sacrifice rituals to ensure rich harvests or a successful hunt.
Something similar can be seen in medicine during antiquity and the Middle Ages. Bloodletting was very much in vogue. If patients survived the procedure, then bloodletting got the credit. And if the patient didn’t survive, the sickness must have been simply too strong to defeat.
In this case, the correlation between the procedure and patient recovery is both spurious and selective.
Fortunately, over the centuries, these crude approaches have given way to more effective treatments based on solid evidence of cause-and-effect.
For evidence-based medicine, the introduction in the mid-20th century of randomized controlled trials marked a major breakthrough. The idea is simple: we compare a test group to a control group. The test group gets the experimental medication or intervention, while the control group gets a placebo. Because we’ve isolated away all other variables, we can make conclusions about the influence of the experimental factor (the only one that’s different).
The equivalent practice for online products is called A/B testing.
A/B testing for verifying causation
You see a correlation between event X and event Y. But to make a decision, you need to know for sure whether there is causation between the two events.
To get the answer, you need to perform an experiment.
For instance, you could give a new product feature to one group of users but not to a second group. All the other features and variables remain the same. Then you collect the data and analyze whether the new feature impacted the metric of interest to you in the first group compared to the second one.
The logic of A/B tests is simple, but actually performing them requires attention to detail and discipline. You have to be careful not to mistake random fluctuation in your target metric for a meaningful change. That’s where statistical significance comes in, which you can read more about here.
Know correlation vs. causation to prevent mistakes and get better product insights
It is extremely easy to mistake correlation for causation when trying to make a product better. This mistake will tend to happen in one of three ways: someone doesn’t know the difference; most often, they know the difference in theory but might fail to notice it in practice; or, sometimes, people even do so deliberately in order to pull the wool over someone else’s eyes.
Cognitive biases, such as confirmation bias and the illusion of control, also contribute to mixing up correlation and causation. Confirmation bias makes us ignore factors that don’t fit into our picture of a phenomenon. The illusion of control can fool us into thinking that we know everything about the product and understand what is causing what.
By seeing the difference between correlation and causation, we can avoid misguided decisions and avoid wasting time and resources.
Experimental confirmation of hypotheses and careful investigation of what causes changes do more than help us to answer a question of interest (for example, why purchase conversions are falling). These important tools also help to understand the product better, resulting in more profound insights and greater product value for users.
Practice now
Test your skills with this quick quiz






